How SMAL dataset show it's correspondence relationship: a guess and a verification

Today, as I delved into a paper on dense shape matching and downloaded the dataset, I found myself interested in how these datasets pertaining to shape matching store correspondences between pairs of shapes. Namely, I am curious about how they preserve the ground truth of these correspondences. Then I chose SMAL dataset to conduct my research on this issue. It’s a dataset containing information on animals.

structure of SMAL dataset

There are two folders in the dataset, one is called correspondences and another, shapes.

shapes

This part is easy to understand, it consists of several $*.obj $ files. For each file, the first line record the total number of the vertices in the file, for example:

1	# nv = 5208

Then next $nv$ lines are information about the coordinates of these vertices, such as:

v 0.406752 0.144386 0.513073
v 0.332418 0.134887 0.600010
v 0.626470 0.261179 0.671501
v 0.621570 0.245227 0.687252
v 0.540259 0.232813 0.785400
v 0.269828 0.402208 0.421639
v 0.239913 0.400150 0.444876
v 0.215629 0.403053 0.444389

Then next $2 nv $ lines stores the information about $2 nv $,

The next $2 * nv $ lines contain information about the triangles, where the$ (1 + nv + i)th$ line stores the three points that form the $ith$ triangle.

For instance,

f 4914 4563 4913
f 1523 574 1524
f 3118 1523 1524
f 4364 1525 4326
f 1529 1526 4363
f 5119 1529 4363
f 4326 1525 1527

correspondences

In this folder, there are also several $.vts $ files, which names are same as the files in *shapes. Each file has n lines of an integer, just like

a simple guess

If the $value-1$ of the $i-th$ -1 of each shape have a one-to-one correspondence. (A)

To illustrate it, think if we have 2 shapes: dog_01 and dog_02.

Then, the 1st line of dog_01.vts is 2425, the 1st line of dog_02.vts is 2363.

If (A) is correct, the the 0 th group of correspondences must be 2424 and 2362(because the index starts from 0, so minus 1)

a simple way to prove

Just draw these two shapes and connect these two points.

If (A) is correct, you can find that these two points should be on the same part of the animal.

code

Here I chose open3d as my visualization tool.

Don’t forget to color the lines or meshes of the shapes, or you can just get a transparent canvas.

Here, I chose 2 group of corresponded points.

import open3d as o3d
import numpy as np
# 加载 OBJ 文件
mesh1 = o3d.io.read_triangle_mesh("dog_01.obj")
mesh2 = o3d.io.read_triangle_mesh("dog_02.obj")

# 设置网格的边缘线颜色为黑色
mesh1.compute_vertex_normals()
mesh2.compute_vertex_normals()
mesh1.paint_uniform_color([0.8, 0.8, 0.8])
mesh2.paint_uniform_color([0.8, 0.8, 0.8])

# 对一个 mesh 进行平移
translation_vector = np.array([1, 0, 0])
mesh2.translate(translation_vector)

# 创建一个可视化窗口
vis = o3d.visualization.Visualizer()
vis.create_window()

# 添加网格到可视化窗口
vis.add_geometry(mesh1)
vis.add_geometry(mesh2)

# 设置网格显示为线框模式
opt = vis.get_render_option()
opt.mesh_show_wireframe = True

# 设置视角
vis.get_view_control().set_front([0, 0, -1])
vis.get_view_control().set_up([0, 1, 0])



line_set = o3d.geometry.LineSet()
points = np.vstack([mesh1.vertices[2424], mesh2.vertices[2362], mesh1.vertices[38], mesh2.vertices[39]])

lines = [[0, 1], [2, 3]]
line_set.points = o3d.utility.Vector3dVector(points)
line_set.lines = o3d.utility.Vector2iVector(lines)

# 将颜色向量转换为 Vector3dVector 类型
colors = [[0, 0, 0] for i in range(len(lines))]
line_set.colors = o3d.utility.Vector3dVector(colors)

vis.add_geometry(line_set)

# 渲染并展示
vis.run()
vis.destroy_window()

results

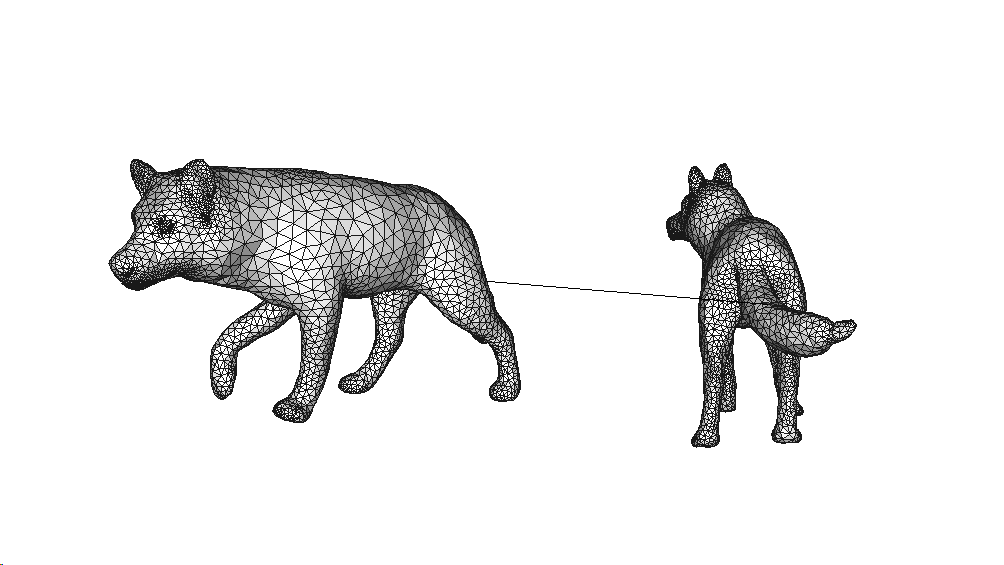
mesh1.vertices[2424], mesh2.vertices[2362]

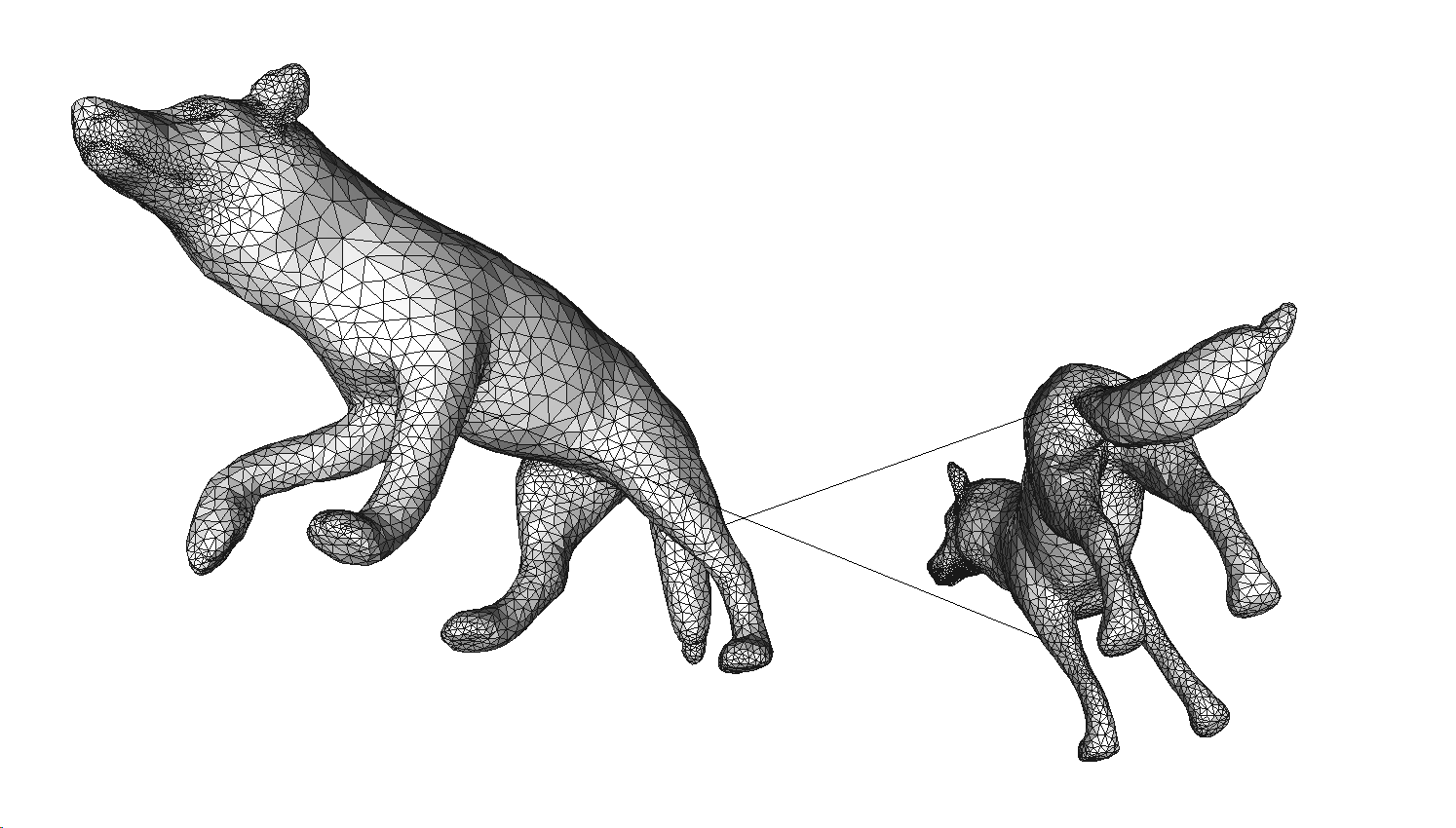
[mesh1.vertices[2424], mesh2.vertices[2362] and mesh1.vertices[38], mesh2.vertices[39]

Thus, it can be find that the first group of points are all on the tails and the second group are all on the left front leg, so this hypothesis is correct.